Présentation :
Dans cet enseignement, les notions de mathématiques sont abordées sous forme de résolution de problèmes.
Cet enseignement est réservé aux élèves qui suivent déjà la spécialité mathématiques en terminale.
L’horaire de mathématiques des élèves est ainsi porté de 6h à 9h.
Grâce à cet enseignement les élève découvrent de nouvelles branches des mathématiques, ce qui leur permet de parfaire leurs connaissances afin de poursuivre leurs études dans des filières scientifiques d’excellence : Classes Préparatoires aux Grandes Ecoles (MPSI, MPI, PCSI ; PTSI, BCPST, ECG), classes préparatoires intégrées, INP, INSA, Cursus Master en Ingénierie ….
Objectifs :
Développer les compétences et connaissances des élèves en mathématiques, autour de trois grands thèmes :
- Les nombres Complexes
- L’arithmétique
- Les matrices et les graphes
Chaque thème est replacé dans son époque. A travers de nombreux points d’histoire des maths, les élèves découvrent des nouvelles notions de la conception, à la formalisation jusqu’à l’utilisation dans les domaines scientifiques actuels.
L’enseignement se fait autour de la résolution de problèmes emblématiques des mathématiques :
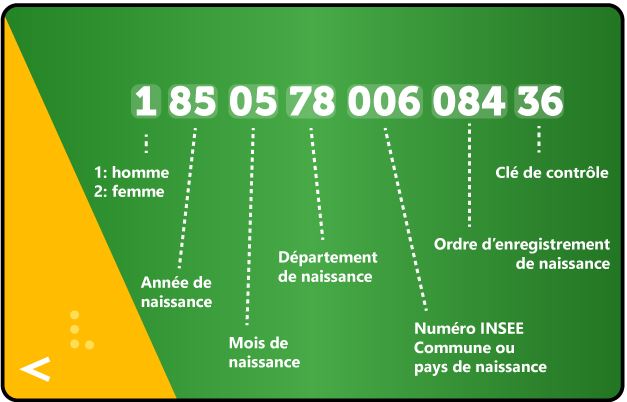
- les codes secrets : du codage affine comme le ROT13 en passant par le numéro INSEE et la méthode de codage RSA utilisée par exemple pour les clés OTP.
- Une infinité de nombres premiers, découverte des nombres de Mersenne, Fermat et Carmichaël.
- Étude du principe de la pertinence d’une page web
- Tartaglia, Cardan et Bombelli : à la recherche de la résolution des équations de degré 3.
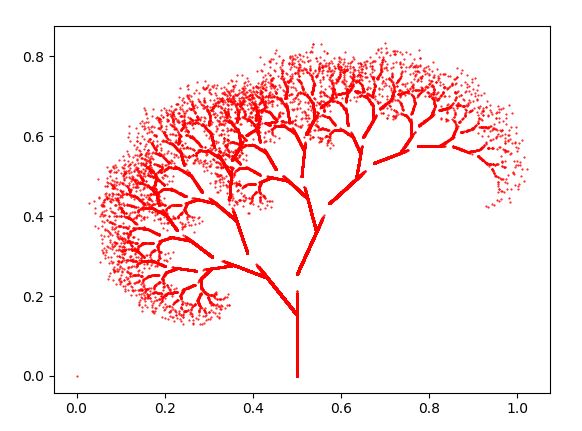
- Itération de polynômes complexes : les fractales
- Le problème du voyageur de commerce
- La découverte de quelques problèmes de Hilbert (les 23 problèmes de Hilbert – Paris – août 1900) non encore résolus de nos jours : la conjecture de Goldbach : « tout nombre entier supérieur à 3 peut s’écrire comme la somme de deux nombres premiers », la conjecture des nombres premiers jumeaux : « il existe une infinité de nombres premiers jumeaux »
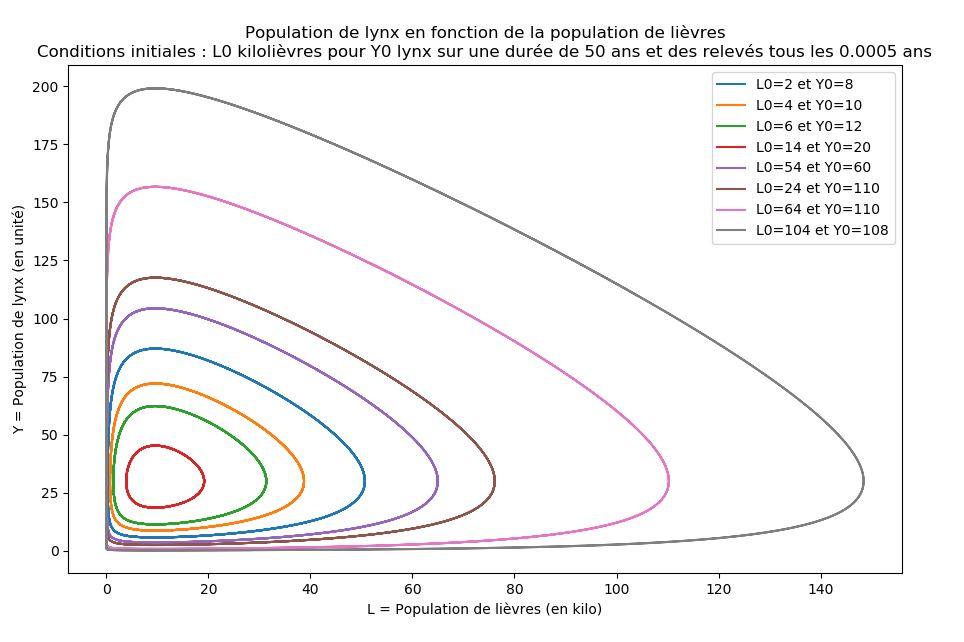
- Le modèle de Lotka-Volterra où comment construire un modèle d’évolution à partir de données expérimentales afin de réguler la pêche, la chasse ou la gestions de faunes sauvages.